Cyclic Redundancy Check (CRC) generation–How to convert a polynomial into a logic circuit that calculates CRC using a parallel equations
April 1, 2014 Leave a comment
This write-up can be supplemented by this article on Wikipedia.
Below is an example of converting CRC-8-ATM polynomial x^8 + x^2 + x + 1 into a parallel circuit for calculating CRC. I’ll first go through the exercise of how the serial implementation works then describe how to derive a parallel circuit.
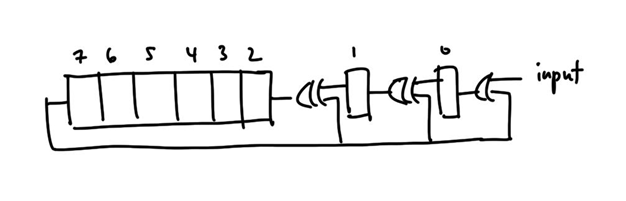
The polynomial (x^8 + x^2 + x + 1) converts into a serial implementation like so…
For the purposes of clarity, I’ll be calling the flops in this circuit crc. Since this circuit has 8-bits of registers, it creates an 8-bit CRC value or crc[7:0]. In order to create the CRC value, the registers are first loaded with an input message followed by trailing zeroes. Using the example from the Wikipedia link above, if the input message was 0101_0111 (0x57), the value shifted into the circuit will be 0101_0111_0000_0000 or (0x5700).
To illustrate using more detail, the table below shows the contents of each crc register bit as we shift the input message and trailing zeroes into the serial circuit. Please note the following:
| crc[7] | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] | crc[0] | input | |
| initial value | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| step 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| step 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| step 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| step 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| step 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| step 6 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| step 7 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| step 8 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| step 9 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| step 10 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| step 11 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| step 12 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| step 13 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| step 14 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| step 15 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| step 16 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
The final CRC value that is taken from row step 16 is 1010_0010 or 0xA2 in hexadecimal.
In order to convert the serial circuit to a parallel version, we need to create Exclusive-OR (XOR) equations for each flop. The symbol for Exclusive-OR is “^”. We can do this my following a similar method (i.e., shifting) as the previous example except that we use variables instead. Using a table as before, we still have an 8-bit register, but this time we will call the input variable in[7:0].
| crc[7] | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] | crc[0] | input | |
| initial value | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | in[7] |
| step 1 | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] ^ crc[7] |
crc[0] ^ crc[7] | in[7] ^ crc[7] | in[6] |
| step 2 | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] ^ crc[7] |
crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] | in[6] ^ crc[6] | in[5] |
| step 3 | crc[4] | crc[3] | crc[2] | crc[1] ^ crc[7] |
crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] | in[5] ^ crc[5] | in[4] |
| step 4 | crc[3] | crc[2] | crc[1] ^ crc[7] |
crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] | in[4] ^ crc[4] | in[3] |
| step 5 | crc[2] | crc[1] ^ crc[7] |
crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] | in[3] ^ crc[3] | in[2] |
| step 6 | crc[1] ^ crc[7] |
crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] ^ crc[2] | in[3] ^ crc[3] ^ crc[2] | in[2] ^ crc[2] | in[1] |
| step 7 | crc[0] ^ crc[7] ^ crc[6] | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] ^ crc[2] | in[3] ^ crc[3] ^ crc[2] ^ crc[1] ^ crc[7] |
in[2] ^ crc[2] ^ crc[1] ^ crc[7] |
in[1] ^ crc[1] ^ crc[7] |
in[0] |
| step 8 | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] ^ crc[2] | in[3] ^ crc[3] ^ crc[2] ^ crc[1] ^ crc[7] |
in[2] ^ crc[2] ^ crc[1] ^ crc[7] ^ crc[0] ^ crc[7] ^ crc[6] |
in[1] ^ crc[1] ^ crc[7] ^ crc[0] ^ crc[7] ^ crc[6] |
in[0] ^ crc[0] ^ crc[7] ^ crc[6] | |
| Removing any duplicate XOR-pairs to simplify | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] ^ crc[2] | in[3] ^ crc[3] ^ crc[2] ^ crc[1] ^ crc[7] |
in[2] ^ crc[2] ^ crc[1] |
in[1] ^ crc[1] |
in[0] ^ crc[0] ^ crc[7] ^ crc[6] | |
| Final equations for each crc flip flop | in[7] ^ crc[7] ^ crc[6] ^ crc[5] | in[6] ^ crc[6] ^ crc[5] ^ crc[4] | in[5] ^ crc[5] ^ crc[4] ^ crc[3] | in[4] ^ crc[4] ^ crc[3] ^ crc[2] | in[3] ^ crc[3] ^ crc[2] ^ crc[1] ^ crc[7] |
in[2] ^ crc[2] ^ crc[1] ^ crc[0] ^ crc[6] |
in[1] ^ crc[1] ^ crc[0] ^ crc[6] |
in[0] ^ crc[0] ^ crc[7] ^ crc[6] |
The Verilog equations would look like the following:
always_comb begin
next_crc[0] = crc[0] ^ crc[6] ^ crc[7] ^ in[0];
next_crc[1] = crc[0] ^ crc[1] ^ crc[6] ^ in[1];
next_crc[2] = crc[0] ^ crc[1] ^ crc[2] ^ crc[6] ^ in[2];
next_crc[3] = crc[1] ^ crc[2] ^ crc[3] ^ crc[7] ^ in[3];
next_crc[4] = crc[2] ^ crc[3] ^ crc[4] ^ in[4];
next_crc[5] = crc[3] ^ crc[4] ^ crc[5] ^ in[5];
next_crc[6] = crc[4] ^ crc[5] ^ crc[6] ^ in[6];
next_crc[7] = crc[5] ^ crc[6] ^ crc[7] ^ in[7];
end
To test that the equations are correct, we apply the input. However, instead of applying the input serially, we apply it in parallel. The input we drive in is 0x5700 or 0101_0111_0000_0000
We first apply the first byte, 0101_0111 (0x57). Note that the initial values of the crc[7:0] register is 0.
| crc[7] | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] | crc[0] | input | |
| 0 ^ 0 ^ 0 ^ 0 | 1 ^ 0 ^ 0 ^ 0 | 0 ^ 0 ^ 0 ^ 0 | 1 ^ 0 ^ 0 ^ 0 | 0 ^ 0 ^ 0 ^ 0 ^ 0 | 1 ^ 0 ^ 0 ^ 0 ^ 0 | 1 ^ 0 ^ 0 ^ 0 | 1 ^ 0 ^ 0 ^ 0 | 0x57 | |
| contents of crc register after input of 0x57 applied | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Next, we apply the second and final byte of trailing zeroes.
| crc[7] | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] | crc[0] | input | |
| 0 ^ 0 ^ 1 ^ 0 | 0 ^ 1 ^ 0 ^ 1 | 0 ^ 0 ^ 1 ^ 0 | 0 ^ 1 ^ 0 ^ 1 | 0 ^ 0 ^ 1 ^ 1 ^ 0 | 0 ^ 1 ^ 1 ^ 1 ^ 1 | 0 ^ 1 ^ 1 ^ 1 | 0 ^ 1 ^ 0 ^ 1 | 0x00 | |
| contents of crc register after input of 0x00 applied | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
The contents of the CRC register is now 1010_0010 or 0xA2, the same value using the serial version of the circuit after we serially shifted in the last 8 bits of trailing zeroes.
In cases where the input bus is larger than the CRC value, we can iterate through the shift register the same number of times as the input bus to create the parallel XOR equations for each crc register bit. Using our previous example, the input bus was 8 bits wide. If the input bus was 16 bits wide, the crc register bus still stays 8-bits wide but the equation changes. I’ll leave it to you, the reader, to figure out how to get the result below.
always_comb begin
next_crc[0] = crc[0] ^ crc[4] ^ crc[6] ^ crc_in[0] ^ crc_in[14] ^ crc_in[15] ^ crc_in[8];
next_crc[1] = crc[1] ^ crc[4] ^ crc[5] ^ crc[6] ^ crc[7] ^ crc_in[14] ^ crc_in[1] ^ crc_in[8] ^ crc_in[9];
next_crc[2] = crc[0] ^ crc[2] ^ crc[4] ^ crc[5] ^ crc[7] ^ crc_in[10] ^ crc_in[14] ^ crc_in[2] ^ crc_in[8] ^ crc_in[9];
next_crc[3] = crc[1] ^ crc[3] ^ crc[5] ^ crc[6] ^ crc_in[10] ^ crc_in[11] ^ crc_in[15] ^ crc_in[3] ^ crc_in[9];
next_crc[4] = crc[0] ^ crc[2] ^ crc[4] ^ crc[6] ^ crc[7] ^ crc_in[10] ^ crc_in[11] ^ crc_in[12] ^ crc_in[4];
next_crc[5] = crc[1] ^ crc[3] ^ crc[5] ^ crc[7] ^ crc_in[11] ^ crc_in[12] ^ crc_in[13] ^ crc_in[5];
next_crc[6] = crc[2] ^ crc[4] ^ crc[6] ^ crc_in[12] ^ crc_in[13] ^ crc_in[14] ^ crc_in[6];
next_crc[7] = crc[3] ^ crc[5] ^ crc[7] ^ crc_in[13] ^ crc_in[14] ^ crc_in[15] ^ crc_in[7];
end
Again, to test if the circuit is working properly, we apply an input of 0101_0111_0000_0000 (0x5700) in one step. Again, the initial value of the flops are zeroes.
| crc[7] | crc[6] | crc[5] | crc[4] | crc[3] | crc[2] | crc[1] | crc[0] | input | |
| 0 ^ 1 ^ 0 ^ 0 | 1 ^ 0 ^ 1 | 0 ^ 1 ^ 0 ^ 0 | 1 ^ 0 ^ 1 ^ 0 | 1 ^ 0 ^ 0 ^ 0 ^ 1 | 1 ^ 1 ^ 0 ^ 1 ^ 1 | 1 ^ 0 ^ 1 ^ 1 | 0 ^ 1 ^ 0 ^ 1 | 0x5700 | |
| contents of crc register after input of 0x5700 applied | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
1010_0010 or 0xA2 is the same answer as the previous examples.
I’ve implemented CRC generators several times but I usually forget how to do it especially when I’ve been working on something else for a long period of time. I’ve documented it here so I don’t forget and to also help my fellow logic designers. Although this may not apply directly to the problem you are trying to solve, I hope you find the process of obtaining the crc logic helpful.